
La notion de modèle est centrale dans la conception et la pratique contemporaines des différents domaines d’investigation auxquels le label « science » a été décerné : physique, chimie, biologie, psychologie, économie, sociologie, etc. En tant qu’intermédiaire entre la théorie et l’expérience, elle constitue un pilier de l’idée de scientificité. Parallèlement, elle s’emploie abondamment pour décrire des organisations sociales : on parle pour un pays de son modèle politique, de son modèle scolaire, pour une entreprise de son modèle économique… Existe-t-il une différence entre ces deux formes d’utilisation du substantif modèle ? En sciences, est-il pertinent d’avoir recours au même mot dans des contextes d’application aussi différents que les interactions atomiques et les interactions sociales ? La multiplicité sémantique du concept de modèle, d’une façon complémentaire du concept de loi, ne contribue-t-elle pas à opérer la jonction entre la science et l’éthique ?
Ces interrogations s’insèrent dans le prolongement des articles sur les concepts de loi, de cause et de raison. Elles débordent le cadre des réflexions sur la sociologie, offrant une perspective plus globale concernant l’idée de science dont les essais de définition se heurtent aux limites des langages, à l’instar de la vérité, sa consœur épistémologique. Dans cet article, nous allons essayer de dégager les grands axes sémantiques, à l’aube du XXe siècle, d’un concept qui a successivement été employé dans des domaines aussi variés que l’architecture, la fabrication d’objets, la peinture, la morale, les sciences expérimentales, les mathématiques ou la logique. Nous nous focaliserons bien entendu sur les significations scientifiques à l’aide du physicien autrichien Ludwig Boltzmann ainsi que du physicien, chimiste, philosophe et historien des sciences Pierre Duhem.
Le concept de modèle avant le XVIIe siècle
Selon la philosophe Suzanne Bachelard « Le terme de modèle vient du latin modulus (diminutif de modus : mesure), terme d’architecture qui désigne la mesure arbitraire servant à établir les rapports de proportion entre les parties d’un ouvrage d’architecture. Le terme de modulus a donné lieu à deux importations successives, au Moyen Âge et à la Renaissance. Tout d’abord modulus a donné en vieux français moule […]. Au XVIe siècle un emprunt à l’italien modello (venant lui-même du latin modulus), employé par la statutaire, a donné en français modèle1 ». Ces origines étymologiques se retrouvent dans les trois grandes acceptions du mot au début du XVIIe siècle2 :
- Ce qui sert ou doit servir d’objet d’imitation pour faire ou reproduire quelque chose (architecture, sculptures, fabriques…) : la maquette, le moule, le prototype.
- Personne ou objet dont l’artiste reproduit l’image.
- Personne, fait, objet possédant au plus haut point certaines qualités ou caractéristiques qui en font le représentant d’une catégorie.
Ces définitions se recoupent en ce que les différents types de modèles concrets ou abstraits (dans le cas des choses de l’esprit) guident l’action, en particulier la production d’objets. Autrement dit, ils sont en grande partie prescriptifs. À partir du XVIIe siècle, les significations du concept de modèle s’étoffent progressivement. L’article « Model », rédigé en 1902 par Ludwig Boltzmann pour l’Encyclopædia Britannica, illustre que les nouvelles conceptions issues des sciences confèrent aux modèles un plus grand rôle descriptif et explicatif ainsi qu’un rôle heuristique.
L’article « Model » de Ludwig Boltzmann
La représentation d’une chose
Dans cet article, Boltzmann définit d’abord le modèle comme une « représentation tangible, de taille égale, plus grande ou plus petite, d’un objet qui existe réellement ou qui doit être construit factuellement ou mentalement. Plus généralement, il désigne une chose, existant réellement ou seulement conçue mentalement, dont les propriétés sont copiées. » L’adjectif « copiées » renvoie à la philosophie antique qui « percevait l’essence du processus de la pensée comme résidant dans le fait que nous attachons aux divers objets réels environnants des attributs physiques particuliers – nos concepts – et nous essayons grâce à ceux-ci de nous représenter les objets dans nos esprits. De telles vues étaient précédemment considérées par les mathématiciens et les physiciens comme rien d’autre que des spéculations stériles, mais J.C. Maxwell, H. v. Helmoltz, E. Mach, H. Hertz et bien d’autres les ont reliées intimement à l’ensemble de la théorie mathématique et physique. Suivant cette perspective, nos pensées entretiennent avec les choses une même relation que les modèles avec les objets qu’ils représentent. »
En quoi consiste plus précisément la relation entre les pensées et les choses ? Boltzmann évoque une « ressemblance » qui « réside principalement dans la nature de la connexion, la corrélation étant analogique à celle obtenue entre la pensée et le langage, le langage et l’écriture, les notes sur la portée et les sons musicaux, etc3. Ici, bien entendu, la symbolisation de la chose constitue le point important bien que, lorsque faisable, la correspondance maximale soit recherchée entre les deux – la gamme de musique, par exemple, étant imitée en plaçant les notes plus haut ou plus bas. » L’analogie est positionnée par Boltzmann au cœur de sa conception de la correspondance entre la pensée et la chose, elle intervient même sous forme arithmétique dans l’expression de la longitude, du kilométrage ou de la température : ces « nombres devraient être envisagés comme des analogies arithmétiques ». Il en va de même concernant la représentation des distances par des lignes ou celle d’évènements temporels par des courbes. Toutefois, dans aucun des cas cités il n’est possible de parler légitimement de modèles car « ceux-ci impliquent toujours une analogie spatiale en trois dimensions ».
Après avoir défini le concept de modèle dans ses grandes lignes, Boltzmann s’interroge sur leur utilité scientifique : « tant que la quantité de sujets à traiter en science était insignifiante, le besoin d’employer des modèles était naturellement moins impératif », notamment parce que les modèles sont « difficiles à faire » et qu’ils ne peuvent pas s’adapter aussi facilement que les symboles de la pensée à des « conditions extrêmement variées ». Cette remarque fait ressortir combien l’idée de modèle était alors associée à des objets tangibles4. Et Boltzmann d’ajouter qu’avec l’accroissement des faits scientifiques, l’économie d’efforts devenait de rigueur pour les comprendre ; « l’établissement ferme de la démonstration oculaire était inévitable étant donné son immense supériorité sur le symbolisme purement abstrait pour l’exposition rapide et complète de relations complexes. »
Malgré cette supériorité de la capacité à visualiser le physicien préconise, d’une part, de s’efforcer à perfectionner l’approche déductive sans l’aide de modèles tangibles et, d’autre part, d’avoir recours à des modèles « objectifs et compréhensifs » pour faciliter les conceptions purement abstraites dans les cas où la quantité de matière à traiter ne peut être appréhendée de façon déductive. L’horizon théorique de Boltzmann est donc celui d’un formalisme déductif que les modèles contribuent à élaborer.
Différents types de modèles
Venons-en aux exemples de modélisations scientifiques employées au début du XXe siècle. On peut distinguer deux grandes typologies de modèles : théoriques et empiriques. Boltzmann choisit de commencer ses illustrations par la première et de la développer bien plus largement même si la seconde s’est historiquement manifestée en premier. Il manifeste ainsi la focalisation sur les modèles théoriques à cette époque. En le suivant, je laisserai de côté les modèles empiriques qui consistaient alors en des modèles réduits/agrandis ou en des prototypes de machines permettant de tester des capacités.
Au sein des modèles théoriques, Boltzmann différencie les modèles stationnaires des modèles dynamiques.

Concernant les modèles stationnaires, il cite en mathématique, et plus spécialement en géométrie, « les modèles faits de papier mâché et de plâtre » principalement utilisés pour « présenter aux sens les formes précises des figures géométriques, des surfaces et des courbes. » En physique il mentionne, outre un exemple en thermodynamique, la modélisation de la réfraction de la lumière dans des cristaux. Il décrit un front d’onde comme « deux tasses ou feuilles étroitement ajustées et exactement l’une à l’intérieur de l’autre ». Ce sont les raies en vert clair sur l’animation ci-dessous :

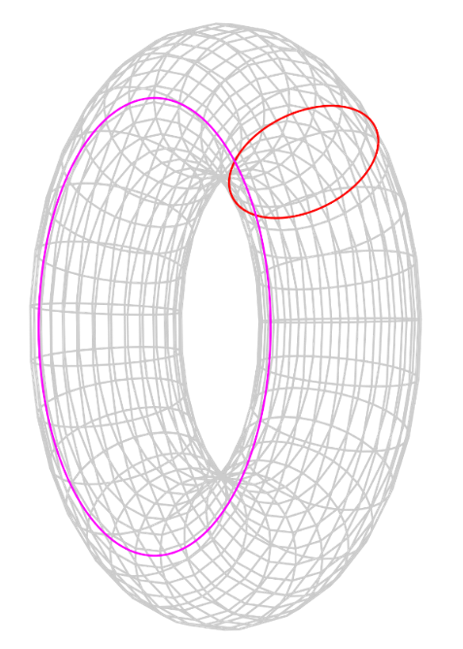
Les modèles dynamiques incluent ceux employés en géométrie pour montrer l’origine de figures géométriques à partir du mouvement de figures tierces, par exemple un tore produit à partir de deux cercles (le cercle rouge se déplaçant ci-dessous tangentiellement au cercle rose). En mécanique et en ingénierie, « une infinie variété de modèles mécaniques est employée pour transmettre à l’œil le mécanisme d’une machine dans son ensemble, ou de ses composants et pièces subalternes. En mécanique théorique, les modèles sont souvent utilisés pour mettre en relief les lois physiques du mouvement dans des cas intéressants ou spéciaux – par exemple, le mouvement d’un corps en train de chuter ou celui d’une toupie, le mouvement d’un pendule à la surface d’une Terre en rotation, le déplacement tourbillonnant de fluides, etc. »
Le modèle mécanique de l’éther de Maxwell
Continuant à réfléchir sur les modèles théoriques, Boltzmann souligne l’importance de la mécanique newtonienne dans les modélisations scientifiques du XIXe siècle. Les phénomènes microscopiques, qu’il s’agisse de la chaleur, de la lumière ou de l’électricité, ont été envisagés comme reposant sur le « mouvement de particules infinitésimales » soumises à des forces analogiques à celles de la mécanique. Cette « première phase de la théorie physique », en « expliquant les phénomènes magnétiques et électriques a inéluctablement été amenée à formuler des hypothèses quelque peu artificielles et improbables, et cela a entraîné J.C. Maxwell […] à proposer une théorie des phénomènes électriques et magnétiques qui était non seulement nouvelle en substance, mais aussi essentiellement différente dans sa forme. Si les molécules et les atomes des anciennes théories n’étaient pas à concevoir comme des points mathématiques abstraits, alors leur nature et leur forme devaient être perçues comme absolument inconnues, et leurs regroupements et leurs mouvements, exigés par la théorie, considérés simplement comme un processus ayant plus ou moins de ressemblance avec le fonctionnement de la nature, et représentant plus ou moins exactement certains de ses aspects. »
Ce passage met en relief que le recours croissant aux modèles dans les pratiques scientifiques du XIXe siècle accompagne une conception moins réaliste des théories qui a été corrélée historiquement avec une appréhension plus précise de la microphysique. L’exemple de Maxwell, qui a unifié les théories existantes de l’électricité et du magnétisme, est intéressant à étudier pour deux raisons : premièrement, l’électromagnétisme constitue un jalon crucial entre la mécanique classique et les théories révolutionnaires du XXe siècle que sont la théorie de la relativité5 et la physique quantique ; deuxièmement, Maxwell est pris pour cible par Pierre Duhem comme nous allons le voir plus loin.
Maxwell a unifié l’électricité et le magnétisme en s’appuyant sur un modèle mécanique de l’éther, le fluide subtil que beaucoup imaginaient au XIXe siècle comme étant le milieu dans lequel se propage la lumière. Ce modèle mécanique est fondé sur une analogie6 entre des tubes de fluide incompressible tourbillonnant et des tubes de flux magnétique (le champ magnétique est analogue au moment cinétique du fluide en rotation). Sur le schéma7 ci-dessous, les tubes sont représentés en coupe transversale par les hexagones. Entre chaque tube figurent de petits cercles blancs, des « roues » dont l’axe de rotation est immobile. Elles représentent les particules électriques. Si ces roues étaient libres de se déplacer, elles porteraient du courant comme dans un milieu conducteur. Elles permettent, dans le modèle, à deux tubes voisins de tourner dans le même sens et assurent un roulement sans glissement parfait.

Ce modèle pour le moins étonnant a été considéré dès son élaboration par Maxwell comme fictionnel : « La conception d’une particule ayant son mouvement connecté à celui de tourbillons par un roulement sans glissement peut apparaître maladroite. Je ne la présente pas comme un mode de connexion existant dans la Nature […]. C’est cependant un mode de connexion qui est mécaniquement concevable et qui permet de mettre en relief les connexions mécaniques réelles entre les phénomènes électromagnétiques connus8. » N’est-il pas intrigant que Maxwell ait réussi à formuler des équations justes à partir d’un modèle qu’il savait irréel ?
Revenons à l’article « Model ». Boltzmann y rappelle que Maxwell « ne croyait pas » aux agents mécaniques de son modèle et qu’il « regardait ceux-ci comme des moyens grâce auxquels les phénomènes peuvent être reproduits ». Tandis que le physicien écossais avait abandonné la quête d’une connaissance exacte de la structure de la matière telle qu’elle est, en Allemagne, G. R. Kirchhoff l’a poursuivie. Celui-ci affirmait que son but était « de décrire, pas d’expliquer le monde phénoménal ». Il a mis l’accent sur les descriptions mathématiques et a estimé que la théorie physique consistait principalement en la construction de formules permettant de fournir la meilleure approximation de la réalité. Un autre physicien que nous avons déjà rencontré, Ernst Mach, tout en attribuant une prééminence moindre aux mathématiques, a mis en avant l’importance de la description en science et plus particulièrement des lois propres à chaque sphère de phénomènes.
Apportons une précision sémantique importante : Kirchhoff et Mach ont privilégié les équations mathématiques qui n’induisent pas nécessairement la possibilité d’identifier des causes, d’où la distinction ferme entre description et explication effectuée par Kirchhoff : l’explication a pour vocation étymologique depuis Racine de discerner les causes et les raisons de phénomènes tandis que la description n’implique pas nécessairement une telle recherche.
En guise de conclusion sur les modèles théoriques, Boltzmann mentionne l’énergétisme, courant de pensée qui s’appuie sur la thermodynamique et ses deux principes fondamentaux : la conservation de l’énergie et la croissance de l’entropie d’un système isolé. Ce courant, pour lequel l’énergie est « la notion fondamentale de toute investigation scientifique », emploie également des analogies qui ne sont pas mécaniques mais se basent sur le comportement de l’énergie dans ses divers modes de manifestation.
Pierre Duhem, critique des modèles
Non réduction et abstraction
Pierre Duhem est affilié à l’énergétisme. Selon lui « La réduction de toutes les propriétés physiques à des combinaisons de figures et de mouvements ou, selon la dénomination en usage, l’explication mécanique de l’Univers, semble aujourd’hui condamnée. Elle n’est pas condamnée par des raisons a priori, métaphysiques ou mathématiques. Elle est condamnée parce qu’elle n’a été jusqu’ici qu’un projet, qu’un rêve, et non une réalité9. » Comme nous venons de l’observer avec l’aide de Boltzmann, la modélisation dans les sciences physiques du XIXe siècle était étroitement associée à la mécanique newtonienne. Duhem doute fortement que les phénomènes microscopiques puissent se réduire à la « Mécanique rationnelle ».
Dans La théorie physique : son objet, sa structure (1906), il expose une conception de la physique reposant principalement sur les lois, la logique et les mathématiques : « Une Théorie physique n’est pas une explication. C’est un système de propositions mathématiques, déduites d’un petit nombre de principes, qui ont pour but de représenter aussi simplement, aussi complètement et aussi exactement que possible, un ensemble de lois expérimentales10. »
Le souci d’économie de principes s’inspire directement de Mach. Ceux-ci « ne prétendent en aucune façon énoncer des relations véritables entre les propriétés réelles des corps. Ces hypothèses peuvent donc être formulées d’une manière arbitraire. La contradiction logique, soit entre les termes d’une même hypothèse, soit entre diverses hypothèses d’une même théorie, est la seule barrière absolument infranchissable devant laquelle s’arrête cet arbitraire11. »
Duhem met donc l’accent sur la logique et les mathématiques, autrement dit les symbolisations abstraites. Dans un fameux passage qui peut sembler par moments davantage politique que scientifique, il oppose à la suite de Pascal les esprits abstraits, forts mais étroits, aux esprits imaginatifs, amples mais faibles. En général, les Français appartiennent à la première catégorie, les Anglais à la seconde. Après avoir donné divers exemples de cette différence de tempérament, il aborde plus particulièrement la question des modèles : ceux-ci foisonnent dans les traités de physique anglais au plus grand étonnement des étudiants français.
Hertz davantage que Maxwell
Duhem s’épanche plus particulièrement sur l’électromagnétisme. Il cite extensivement William Thomson (Lord Kelvin) faisant l’apologie des modèles mécaniques et plus spécialement de ceux de Maxwell, puis il commente : « Comprendre un phénomène physique, c’est donc, pour les physiciens de l’École anglaise, composer un modèle qui imite ce phénomène ; dès lors, comprendre la nature des choses matérielles, ce sera imaginer un mécanisme dont le jeu représentera, simulera, les propriétés des corps ; l’École anglaise est acquise entièrement aux explications purement mécaniques des phénomènes physiques12. »
Si Newton fait figure d’exception, car il a prôné une théorie « purement abstraite », Duhem estime qu’un physicien anglais construisant un modèle « ne s’embarrasse d’aucun principe cosmologique, il ne s’astreint à aucune exigence logique. Il ne cherche pas à déduire son modèle d’un système philosophique ni même à le mettre d’accord avec un tel système. Il n’a qu’un objet : créer une image visible et palpable des lois abstraites que son esprit ne pourrait saisir sans le secours de ce modèle13. »
C’est notamment le cas du Traité d’Électricité et de Magnétisme de Maxwell qui « n’est un système logique » ; « il se compose d’une suite de modèles, dont chacun figure un groupe de lois, sans souci des autres modèles qui ont servi à figurer d’autres lois14 ». Si Duhem perçoit en Maxwell un « grand physicien15 », il déplore la réduction de la théorie physique à une « collection de modèles » et préfère convier Heinrich Hertz qui a apporté la confirmation expérimentale des ondes électromagnétiques et qui a écrit : « La théorie de Maxwell, ce sont les équations de Maxwell16. »
Analogie et modèle
Bien que Duhem valorise considérablement la théorie abstraite, on pourrait songer qu’il accorde aux modèles une fonction heuristique, c’est-à-dire facilitatrice de découvertes. Il ne daigne même pas leur faire cette concession, la juxtaposition de modèles étant corrélée à « l’abandon du souci d’unité logique17 ». Pire, dans de nombreux cas d’une théorie déjà formée, le modèle relègue « dans l’oubli la théorie abstraite qui l’avait précédé et sans laquelle il n’eût point été imaginé18. »
Pour apprécier l’éventuelle fécondité des modèles, Duhem enjoint de ne pas confondre ceux-ci avec l’usage de l’analogie. Selon lui, cette dernière « a peut-être été, de tous les procédés mis en œuvre pour construire des théories physiques, la méthode la plus sûre et la plus féconde19. » Il convoque d’ailleurs Maxwell pour définir l’analogie : « Par analogie physique j’entends cette ressemblance partielle entre les lois d’une science et les lois d’une autre science qui fait que l’une des deux sciences peut servir à illustrer l’autre20. »
Duhem fournit à titre d’exemple l’analogie entre les phénomènes sonores et ceux produits par la lumière « qui a fourni la notion d’onde lumineuse dont Huygens a su tirer un merveilleux parti21 » ; il mentionne la « similitude entrevue entre la propagation de la chaleur et la propagation de l’électricité au sein des conducteurs » qui a permis à Ohm de transposer du premier domaine au second les équations de Fourier.
L’analogie intervient donc selon Duhem entre « deux groupes de lois physiques ou entre deux théories distinctes ». Elle consiste « à rapprocher l’un de l’autre deux systèmes abstraits22 ». Elle opère donc à un niveau abstrait tandis que le modèle relève de l’imagination. C’est pourquoi il ne paraît pas à Duhem que le modèle mécanique de l’éther imaginé par Maxwell l’ « ait aidé » à créer la théorie de l’électromagnétisme. « Sans doute il s’efforce de tirer de ce modèle les deux formules essentielles de cette théorie ; mais la manière même dont il dirige ses tentatives montre du reste que les résultats à obtenir lui étaient connus par ailleurs23 ».
L’approche de Duhem est polémique voire excessive, privilégiant la théorie abstraite, la logique et les mathématiques au détriment des modèles. En particulier, elle réduit l’analogie à des rapports entre systèmes abstraits alors que Maxwell a produit des modèles s’appuyant sur des analogies entre des phénomènes empiriques (champ magnétique et moment cinétique, roues et particules électriques…). Bien qu’excessive, elle rejoint l’analyse de Boltzmann qui associe étroitement modélisation et sensations : les modèles permettent de voir un aspect de la théorie, de s’en former une image, un aperçu. Cette manière d’envisager les modèles scientifiques, comme nous le verrons, va sensiblement se métamorphoser au cours du XXe siècle.
Notes
1.↑ Suzanne Bachelard, « Aspects historiques des notions » inÉlaboration et justification des modèles: applications en biologie : actes du colloque présentés par P. Delattre et M. Thellier, Volume 1, Maloine, 1979, p. 15.
2.↑ Les définitions proviennent du Grand Robert, elles sont recoupées avec celles du Littré.
3.↑ Je souligne.
4.↑ C’est ce qu’estime Daniela M. Bailer Jones dans Scientific Models in Philosophy of Science, University of Pittsburgh Press, 2009, p. 27-28.
5.↑ Selon Einstein, le changement dans la conception de la réalité occasionné par Maxwell « est le plus profond et le plus fructueux que la physique ait vécu depuis le temps de Newton. » Cité par Longair M. 2015 ‘…a paper …I hold to be great guns’: a commentary on Maxwell (1865) ‘A dynamical theory of the electromagnetic field’. Phil. Trans. R. Soc. A 373: 20140473. http://dx.doi.org/10.1098/rsta.2014.0473.
6.↑ Ibid. Voir aussi Margaret Morrison, « Fictions, Représentations, and Reality » in Mauricio Suárez (dir.), Fictions in Science, Routledge, 2008.
7.↑ Ibid. Schéma extrait de Maxwell, On Physical Lines of Force, 1861.
8.↑ Ibid. J’ai traduit « perfect rolling contact » par « roulement sans glissement » afin de faciliter la compréhension.
9.↑ Pierre Duhem, Traité d’énergétique ou de thermodynamique générale, Tome 1, Gauthier-Villars, 1911, p. 2.
10.↑ Pierre Duhem, La théorie physique : son objet, sa structure, Vrin, 2015 (1906), p. 44.
11.↑ Ibid.
12.↑ Ibid., p. 111.
13.↑ Ibid., p. 113.
14.↑ Ibid., p. 129.
15.↑ Ibid., p. 134.
16.↑ Ibid.
17.↑ Ibid., p. 139.
18.↑ Ibid., p. 140.
19.↑ Ibid., p. 142.
20.↑ J.C. Maxwell, Scientific Papers, vol. I, p. 156 in Ibid.
21.↑ Ibid.
22.↑ Ibid., p. 143. Je souligne.
23.↑ Ibid., p. 144.